
- MEASURING THE ACCELERATION DUE TO GRAVITY LAB HOW TO
- MEASURING THE ACCELERATION DUE TO GRAVITY LAB FULL
- MEASURING THE ACCELERATION DUE TO GRAVITY LAB SERIES

The two large balls could be positioned either away from or to either side of the torsion balance rod. ĭetail showing torsion balance arm ( m), large ball ( W), small ball ( x), and isolating box ( ABCDE).
MEASURING THE ACCELERATION DUE TO GRAVITY LAB SERIES
Cavendish then carried out a series of measurements with the equipment and reported his results in the Philosophical Transactions of the Royal Society in 1798. After his death the apparatus passed to Francis John Hyde Wollaston and then to Cavendish, who rebuilt the apparatus but kept close to Michell's original plan. However, Michell died in 1793 without completing the work. The experiment was devised sometime before 1783 by geologist John Michell, who constructed a torsion balance apparatus for it. His experiment gave the first accurate values for these geophysical constants. Instead, the result was originally expressed as the specific gravity of Earth, or equivalently the mass of Earth. Because of the unit conventions then in use, the gravitational constant does not appear explicitly in Cavendish's work. unless there was some kind of consistent error in the timing process such as being faster at pressing start than in pressing stop due to anticipating the end of the tenth swing.The Cavendish experiment, performed in 1797–1798 by English scientist Henry Cavendish, was the first experiment to measure the force of gravity between masses in the laboratory and the first to yield accurate values for the gravitational constant. Of course your average over 30 swings should reduce your error by a factor of sqrt(30). Try increasing or decreasing your average time by that much and see how it affects the result. If you time something known to be very accurate, like a clock second had, you will probably find an error of something like 0.1 second. The stopwatch is very accurate, so your main error is going to be due to hitting the button at the wrong time. It would be interesting to try to estimate the accuracy of your time measurements and perhaps deduce from that the accuracy of the calculated value for g.

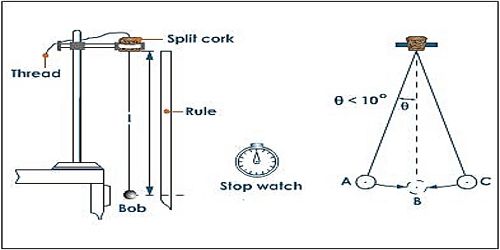
That's why it is important to go to great lengths to measure the time accurately. Note that the time measurement is squared, so its error strongly affects the result. Students often get 9.6 to 10 m/s² from this experiment because air resistance, etc. 1 to the length, you would have 8.9 instead of 8.0 for your answer. Find the average time: Test case 1: 23.41s/10 =2.341 seconds per cycle. So i did make an attempt, can someone check if i am doing it right and if my answer seem fine for all questions.
MEASURING THE ACCELERATION DUE TO GRAVITY LAB HOW TO
I don't know how to do average time, and if i get the average time wrong then i get number 2 wrong and then my answer for number 3 will be wrong. Using the period of the pendulum and its length, calculate the value of "g". Using this average time, calculate the period of the pendulum.
MEASURING THE ACCELERATION DUE TO GRAVITY LAB FULL
Test case 3- time it took for the pendulum to complete 10 full cycles is 23.44 s. Test case 2- time it took for the pendulum to complete 10 full cycles is 23.41 s. Test case 1- time it took for the pendulum to complete 10 full cycles is 23.41 s. This lab is done assuming, there is no air resistance or any other force other than just gravity. We let it go from 20 degrees and counted 10 cycles and recorded how much time it took for the pendulum to complete 10 cycles. We did a lab using a pendulum attached to a string about 1.12m long.


 0 kommentar(er)
0 kommentar(er)
